Generalized singular value decomposition
In linear algebra the generalized singular value decomposition (GSVD) is a matrix decomposition more general than the singular value decomposition. It is used to study the conditioning and regularization of linear systems with respect to quadratic semi-norms.
Given an 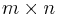 matrix
matrix  and a
and a 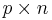 matrix
matrix  of real or complex numbers the GSVD is
of real or complex numbers the GSVD is
and
where 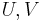 and
and  are unitary matrices and
are unitary matrices and  is an upper triangular, nonsingular
is an upper triangular, nonsingular  matrix, and
matrix, and 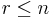 is the rank of
is the rank of ![[A^*,B^*]](/2012-wikipedia_en_all_nopic_01_2012/I/f2e4f4cd3bf7965bfdb8946b247d8212.png) . Also,
. Also, 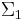 and
and 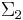 are
are 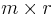 and
and 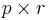 matrices, zero except for the leading diagonals which consist of the real numbers
matrices, zero except for the leading diagonals which consist of the real numbers 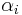 and
and 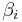 respectively, satisfying
respectively, satisfying
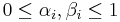 and
and 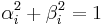 .
.
The ratios 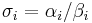 are analogous to the singular values. In the important special case, where
are analogous to the singular values. In the important special case, where  is square and invertible, they are the singular values, and
is square and invertible, they are the singular values, and  and
and  are the matrices of singular vectors, of the matrix
are the matrices of singular vectors, of the matrix 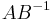 .
.
References
- Gene Golub, and Charles Van Loan, Matrix Computations, Third Edition, Johns Hopkins University Press, Baltimore, 1996, ISBN 0-8018-5414-8
- Hansen, Per Christian, Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion, SIAM Monographs on Mathematical Modeling and Computation 4. ISBN 0-89871-403-6
- LAPACK manual [1]
- GSVD in Genomic Signal Processing [2]
![A=U\Sigma_1 [ 0, R] Q^*](/2012-wikipedia_en_all_nopic_01_2012/I/31b2a052fda1ee358ae791b87a3bfcda.png)
![B=V\Sigma_2 [ 0, R] Q^*](/2012-wikipedia_en_all_nopic_01_2012/I/f6c3e1b0198b0f4bc26f0bc5dad209f6.png)